導(dǎo)讀：

不少科普作品說量子密碼術(shù)離不開量子糾纏,，這就大錯(cuò)特錯(cuò)了,！實(shí)際上，量子密碼術(shù)有若干種實(shí)現(xiàn)方案,，有些用到量子糾纏,，有些不用量子糾纏,。對(duì)于實(shí)驗(yàn)來說,，操縱多個(gè)粒子肯定比操縱一個(gè)粒子困難。所以,，用單粒子方案,，也就是說不用量子糾纏，才能達(dá)到最優(yōu)的效果,。

前文參見：

你完全可以理解量子信息（1） | 袁嵐峰

你完全可以理解量子信息（2-3） | 袁嵐峰

你完全可以理解量子信息（4-5） | 袁嵐峰）

你完全可以理解量子信息（6） | 袁嵐峰）

你完全可以理解量子信息（7） | 袁嵐峰

你完全可以理解量子信息（8-10）| 袁嵐峰

你完全可以理解量子信息（11-12）| 袁嵐峰

你完全可以理解量子信息（13）| 袁嵐峰

十四,、量子密碼術(shù)的實(shí)現(xiàn)方法

什么樣的操作，能在通信雙方產(chǎn)生一段相同的隨機(jī)數(shù)序列呢,？

如果你是一個(gè)真正聰明而細(xì)心的讀者,，你就會(huì)想起本文前面關(guān)于EPR實(shí)驗(yàn)的一句話（http://weibo.com/ttarticle/p/show?id=2309404152264544625278）：“A測(cè)量粒子1得到的是一個(gè)隨機(jī)數(shù)，B測(cè)量粒子2得到的也是一個(gè)隨機(jī)數(shù),，只不過這兩個(gè)隨機(jī)數(shù)必然相等而已,。”

妙?。∧且欢问墙忉尀槭裁碋PR實(shí)驗(yàn)不能傳輸信息,，但有了量子密碼術(shù)的背景知識(shí),，你就會(huì)領(lǐng)悟到，把這個(gè)過程重復(fù)多次,，雙方得到的相同的隨機(jī)數(shù)序列就可以用作密鑰,。然后你可以用這個(gè)密鑰傳輸信息。這和“EPR實(shí)驗(yàn)不傳輸信息”并不矛盾,，因?yàn)閭鬏斝畔r(shí)用的是普通的通信方式,，不是EPR實(shí)驗(yàn)。

很好,，利用量子糾纏,，我們立刻就找到了一種量子密碼術(shù)的方案。這至少說明量子密碼術(shù)是可以實(shí)現(xiàn)的,，證明了它的存在性,。

量子密碼術(shù)

但是，不少科普作品說量子密碼術(shù)離不開量子糾纏,，這就大錯(cuò)特錯(cuò)了,！這種說法造成了很多困擾。實(shí)際上,，量子密碼術(shù)有若干種實(shí)現(xiàn)方案,，有些用到量子糾纏，有些不用量子糾纏,。量子糾纏是個(gè)可選項(xiàng)，而不是必要條件,。

不僅如此,，稍微想想你還會(huì)明白，量子糾纏是一種多粒子體系的現(xiàn)象,，而對(duì)于實(shí)驗(yàn)來說,，操縱多個(gè)粒子肯定比操縱一個(gè)粒子困難。所以,，只要有單粒子的方案,，人們必然會(huì)優(yōu)先用單粒子方案。實(shí)際情況正是如此,，絕大多數(shù)量子密碼術(shù)的實(shí)驗(yàn)都是用單粒子方案做的,，這樣才能達(dá)到最優(yōu)的效果。而基于量子糾纏的量子密碼術(shù)方案,，就像用火箭送快遞一樣不實(shí)用,，只具有理論意義,。

當(dāng)然，這不是說量子糾纏沒用,。對(duì)于整個(gè)量子信息學(xué)科來說,，量子糾纏非常有用，例如量子隱形傳態(tài)就以量子糾纏為基礎(chǔ),，但那是量子密碼術(shù)之外的應(yīng)用了,。正是因?yàn)榱孔用艽a術(shù)可以不用量子糾纏，所以它的技術(shù)難度在量子信息的各種應(yīng)用中是最低的（只是相對(duì)而言,，絕對(duì)的難度還是很高）,，所以它發(fā)展得最快，最先接近了產(chǎn)業(yè)化,。

不用量子糾纏,，怎么在雙方產(chǎn)生相同的隨機(jī)數(shù)序列？想想前面介紹的“三大奧義”,，真正產(chǎn)生隨機(jī)數(shù)的是對(duì)疊加態(tài)的測(cè)量,。所以只要充分利用疊加和測(cè)量這兩個(gè)手段，單個(gè)粒子就可以在雙方產(chǎn)生相同的隨機(jī)數(shù),。在“三大奧義”中,，量子密碼術(shù)只需要前兩個(gè)（疊加、測(cè)量）就夠了,，不需要第三個(gè)（糾纏）,。

科學(xué)家們把量子密碼術(shù)的方案都稱為某某協(xié)議（就像計(jì)算機(jī)科學(xué)中的“TCP/IP協(xié)議”），上述利用EPR對(duì)的方案叫做EPR協(xié)議,，而單粒子的方案包括BB84協(xié)議,、B92協(xié)議、誘騙態(tài)協(xié)議等等,。BB84協(xié)議是美國(guó)科學(xué)家Charles H. Bennett和加拿大科學(xué)家Gilles Brassard在1984年提出的,，BB84是兩人姓的首字母以及年份的縮寫。BB84協(xié)議是最早的一個(gè)方案,，而且目前最先進(jìn)的誘騙態(tài)協(xié)議可以理解為它的推廣,。所以只要理解了BB84協(xié)議，就理解了量子密碼術(shù)的精髓,。

在BB84協(xié)議中,，用到光子的四個(gè)狀態(tài)：|0>、|1>,、|+>和|->,。Hi，四位老朋友,，又見面了~（|0>,、|1>,、|+>和|->：我們叫做“江南四大才子”！）在實(shí)驗(yàn)上,，這四個(gè)狀態(tài)是用光子的偏振（回顧一下,，偏振方向就是電場(chǎng)所在的方向）來表示的，分別對(duì)應(yīng)光子的偏振處于0度,、90度,、45度和135度。

江南四大才子

讓我們回憶一下,，|0>和|1>這兩個(gè)態(tài)構(gòu)成一個(gè)基組,，|+>和|->這兩個(gè)態(tài)構(gòu)成另一個(gè)基組。在某個(gè)基組下測(cè)量這個(gè)基組中的狀態(tài),，比如說在|0>和|1>的基組中測(cè)量|0>,，那么結(jié)果不變，測(cè)完以后還是|0>這個(gè)態(tài),。在某個(gè)基組下測(cè)量這個(gè)基組之外的狀態(tài),，比如說在|0>和|1>的基組中測(cè)量|+>，那么結(jié)果必然改變,，以一半的概率變成|0>,，一半的概率變成|1>。

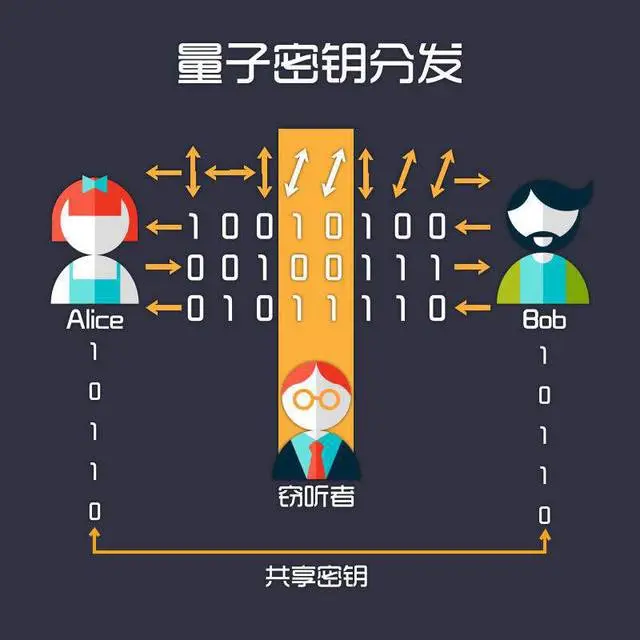
好,，現(xiàn)在我們來敘述BB84協(xié)議的操作過程,。A拿一個(gè)隨機(jī)數(shù)發(fā)生器（通俗地說就是擲硬幣），產(chǎn)生一個(gè)隨機(jī)數(shù)0或者1（讓我們把它記作a）,，根據(jù)這個(gè)隨機(jī)數(shù)決定選擇哪個(gè)基組：得到0就用|0>和|1>的基組,，得到1就用|+>和|->的基組。選定基組之后,，再產(chǎn)生一個(gè)隨機(jī)數(shù)（記作a′）,，根據(jù)這第二個(gè)隨機(jī)數(shù)決定在基組中選擇哪個(gè)狀態(tài)：得到0就在|0>和|1>中選擇|0>或者在|+>和|->中選擇|+>，得到1就在|0>和|1>中選擇|1>或者在|+>和|->中選擇|->,。經(jīng)過這樣雙重的隨機(jī)選擇之后，A把選定狀態(tài)的光子發(fā)送出去,。

B收到光子的時(shí)候,，并不知道它屬于哪個(gè)基組。他怎么辦呢,？他可以猜測(cè),。B也拿一個(gè)隨機(jī)數(shù)發(fā)生器，產(chǎn)生一個(gè)隨機(jī)數(shù)（記作b）,，得到0的時(shí)候就在|0>和|1>的基組中測(cè)量,，得到1的時(shí)候就在|+>和|->的基組中測(cè)量,。B測(cè)得|0>或者|+>就記下一個(gè)0，測(cè)得|1>或者|->就記下一個(gè)1,，我們把這個(gè)數(shù)記為b′,。

看出來了吧？如果B猜對(duì)了基組,，a = b,，那么光子的狀態(tài)就是B的基組中的一個(gè)，所以測(cè)量以后不會(huì)變,，a′必然等于b′,。而如果B猜錯(cuò)了基組，a ≠ b,，那么光子的狀態(tài)就不是B的基組中的一個(gè),，所以測(cè)量后會(huì)突變，a′和b′就不一定相等了（有一半的概率不同）,。

把這樣的操作重復(fù)若干次,，雙方發(fā)送和測(cè)量若干個(gè)光子。結(jié)束后,，雙方公布自己的a和b隨機(jī)數(shù)序列（“公布”的意思就是對(duì)全世界公開,，就是這么任性~），比如說a的序列是0110,，b的序列是1100,。然后找出其中相同的部分，在這個(gè)例子里就是第二位（1）和第四位（0）,。

現(xiàn)在我們知道了,，在第二位和第四位，a′和b′必然是相同的,！A和B把各自手里第二位和第四位的a′和b′記下來,，這個(gè)隨機(jī)數(shù)序列就可以用作密鑰。如果發(fā)送和接收n個(gè)光子,，由于B猜對(duì)基組的概率是一半,，就會(huì)產(chǎn)生一個(gè)長(zhǎng)度約為n/2位的密鑰。至于a,、b兩個(gè)序列中不同的部分,，在這個(gè)例子中就是第一位（0對(duì)1）和第三位（1對(duì)0），它們對(duì)應(yīng)的a′和b′有可能不同,，所以我們就不去看它們了,，這部分?jǐn)?shù)據(jù)直接拋棄。

不過,，到目前為止我們都假定只有A,、B雙方在通信,，沒有敵對(duì)方在竊聽。作為一個(gè)保密的方法,，需要回答的下一個(gè)問題是：在有人竊聽的情況下,，如何保證密鑰不被偷走？

讓我們把這個(gè)竊聽者稱為E（聯(lián)想英文單詞evil,，“邪惡的”）,。料敵從寬，我們還假設(shè)E非常神通廣大,，A發(fā)給B的每一個(gè)光子都先落到了他手里,。BB84協(xié)議有一個(gè)辦法，使得即使在這種最不利的情況下,，E也偷不走情報(bào),。

量子密鑰分發(fā)

什么辦法呢？站在E的角度上想一想,。如果E只是把這個(gè)光子拿走,，那么他只是阻斷了A、B之間的通信,，仍然拿不到任何信息,。E希望的是，自己知道這個(gè)光子的狀態(tài),，然后把這個(gè)光子放過去,，讓B去接收。這樣A和B看不出任何異樣,，不知道E在竊聽,，而在A和B公布a和b序列后，E看自己手上的光子狀態(tài)序列,，也就知道了他們的密鑰,。

但是E的困難在于，他要知道當(dāng)前這個(gè)光子處在什么狀態(tài),，就要做測(cè)量,。可是他不知道該用哪個(gè)基組測(cè)量,，那么他只能猜測(cè),。這就有一半的概率猜錯(cuò)，猜錯(cuò)以后就會(huì)改變光子的狀態(tài),。

例如A發(fā)出的狀態(tài)是|+>（這對(duì)應(yīng)于a= 1, a′ = 0）,，E用|0>和|1>的基組來測(cè)量|+>,，就會(huì)以一半的概率把它變成|0>,，一半的概率把它變成|1>,，然后B再去測(cè)量這個(gè)光子。如果B用的基組是|0>和|1>（b = 0）,，公布后會(huì)發(fā)現(xiàn)這里a ≠ b,，這個(gè)數(shù)據(jù)就被拋棄。而如果B用的基組是|+>和|->（b = 1）,，公布后會(huì)發(fā)現(xiàn)這里a = b, 這個(gè)數(shù)據(jù)要保留,。這時(shí)b′等于什么呢？無論是|0>還是|1>,，在|+>和|->的基組下測(cè)量時(shí)都以一半的概率變成|+>（b′ = 0）,，一半的概率變成|->（b′ = 1）。因此,，a′和b′有一半的概率出現(xiàn)不同,。

稍微想一下，你就會(huì)發(fā)現(xiàn)這是普遍的結(jié)果：只要E猜錯(cuò)了基組,，a′和b′就會(huì)有一半的概率不同,。E猜錯(cuò)基組的概率是一半，所以總而言之,，在E做了測(cè)量的情況下a′和b′不同的概率是1/2 × 1/2= 1/4,。這就是竊聽行為的蛛絲馬跡。

那么,，通信方的應(yīng)對(duì)策略就呼之欲出了,。為了知道有沒有竊聽，A和B在得到a′和b′序列后,，再挑選一段公布,。這是BB84協(xié)議中的第二次公布。你看,，有時(shí)為了保密,，我們必須要“公布”，而且“公布”會(huì)成為一個(gè)威力巨大的保密武器,。假如在公布的序列中出現(xiàn)了不同,，那么他們就知道有人在竊聽，這次通信作廢,。

這樣做的效率怎么樣呢,？公布一個(gè)字符，E蒙混過關(guān)的幾率是3/4,。公布兩個(gè)字符,，就是3/4的平方。如果公布m個(gè)字符，E蒙混過關(guān)的概率就是3/4的m次方,。這個(gè)概率隨著m的增加迅速接近于0,，例如當(dāng)m = 100時(shí)，只剩下3.2× 10-13,。因此,，如果公布了很長(zhǎng)一段都完全相同，那么就可以以接近100%的置信度確認(rèn)沒有竊聽,，通信雙方就把a(bǔ)′和b′序列中剩下的部分作為密鑰,。

如果發(fā)現(xiàn)有竊聽，那么該怎么辦,？如果有多條信道的話,，你可以換一條信道，除非敵人把所有的信道都卡死了,。此外,，量子密碼術(shù)跟一些光學(xué)技術(shù)聯(lián)用，可以確定竊聽者的位置,，所以你可以通知警察,、國(guó)安、軍隊(duì),，把竊聽者抓起來,。這是量子密碼術(shù)特有的一個(gè)巨大優(yōu)勢(shì)，傳統(tǒng)密碼術(shù)首先就發(fā)現(xiàn)不了竊聽,，更不用說定位了,。不過這是安全部門的任務(wù)，不屬于密碼術(shù)的范圍,。至于密碼術(shù)本身,，在發(fā)現(xiàn)竊聽時(shí)唯一能做的就是停止通信。因此,，量子密碼術(shù)規(guī)定在發(fā)現(xiàn)竊聽時(shí)停止通信,，就像諜戰(zhàn)片里通信員被發(fā)現(xiàn)時(shí)第一件事就是把密碼本銷毀。這樣就不會(huì)生成密鑰,，也不會(huì)發(fā)送密文,，自然也就不會(huì)泄密。因此,，即使在最不利的情況下,，量子密碼術(shù)也可以保證不泄密。

媒體經(jīng)常用“絕對(duì)安全”或“無條件安全”或諸如此類的說法,，來形容量子密碼術(shù),。以前這些詞看著一頭霧水,，現(xiàn)在你可以理解，量子密碼術(shù)的安全性表現(xiàn)在五個(gè)方面：一,，密文即使被截獲了也不會(huì)被破譯,；二，不會(huì)被計(jì)算技術(shù)的進(jìn)步破解,；三，沒有傳遞密鑰的信使,；四,，可以在每次使用前現(xiàn)場(chǎng)產(chǎn)生密鑰，平時(shí)不需要保存密鑰,；五,，在密鑰生成過程中如果有人竊聽，會(huì)被通信方發(fā)現(xiàn),。這幾點(diǎn)是量子密碼術(shù)的本質(zhì)特點(diǎn),，任何協(xié)議都是如此。

在這五個(gè)方面,，傳統(tǒng)密碼術(shù)做得怎么樣呢,？從前面的介紹可以看出，傳統(tǒng)密碼術(shù)或者只能滿足第一點(diǎn),、第三點(diǎn)和第四點(diǎn)（非對(duì)稱密碼體制,，第一點(diǎn)依賴于數(shù)學(xué)復(fù)雜性，不是嚴(yán)格滿足的）,，或者只能滿足第一點(diǎn)和第二點(diǎn)（對(duì)稱密碼體制）,，無論如何都無法滿足第五點(diǎn)。量子密碼術(shù)是目前所知唯一的既不需要信使,、也不懼怕算法進(jìn)步的保密方法,，更是唯一的能發(fā)現(xiàn)竊聽的保密方法。一對(duì)比,，就知道量子密碼術(shù)的優(yōu)勢(shì)有多大了,！

量子密碼術(shù)的安全性是物理原理的產(chǎn)物，建立在量子力學(xué)的基礎(chǔ)上,。在有些人看來,，量子力學(xué)似乎不是一個(gè)非常可靠的基礎(chǔ),。這種心理可以理解,，因?yàn)榫拖瘛叭髪W義”顯示的，量子力學(xué)跟日常生活經(jīng)驗(yàn)反差巨大,，不是一個(gè)很容易接受的理論,。但如果你想為了破解量子密碼術(shù)而推翻量子力學(xué),，那就掉到一個(gè)巨坑里去了。如前所述,，量子力學(xué)經(jīng)過了上百年的考驗(yàn),，其應(yīng)用遍及現(xiàn)代生活的所有角落。如果你懷疑量子力學(xué)的原理,，那么你是不是應(yīng)該先擔(dān)心自己的電腦不能工作,、自己的手機(jī)打不出去呢？

對(duì)于軍事和金融這樣急需保密的領(lǐng)域,，量子密碼術(shù)顯然具有非常高的戰(zhàn)略意義,。如果說可以破解公鑰密碼體系的量子計(jì)算機(jī)是最強(qiáng)的矛，那么能夠抵御一切攻擊的量子密碼術(shù)就是最強(qiáng)的盾,。以子之矛攻子之盾,，誰(shuí)勝？盾勝,！

（未完待續(xù)）

背景簡(jiǎn)介：本文作者為袁嵐峰,，中國(guó)科學(xué)技術(shù)大學(xué)化學(xué)博士，中國(guó)科學(xué)技術(shù)大學(xué)合肥微尺度物質(zhì)科學(xué)國(guó)家實(shí)驗(yàn)室副研究員,，科技與戰(zhàn)略風(fēng)云學(xué)會(huì)會(huì)長(zhǎng)