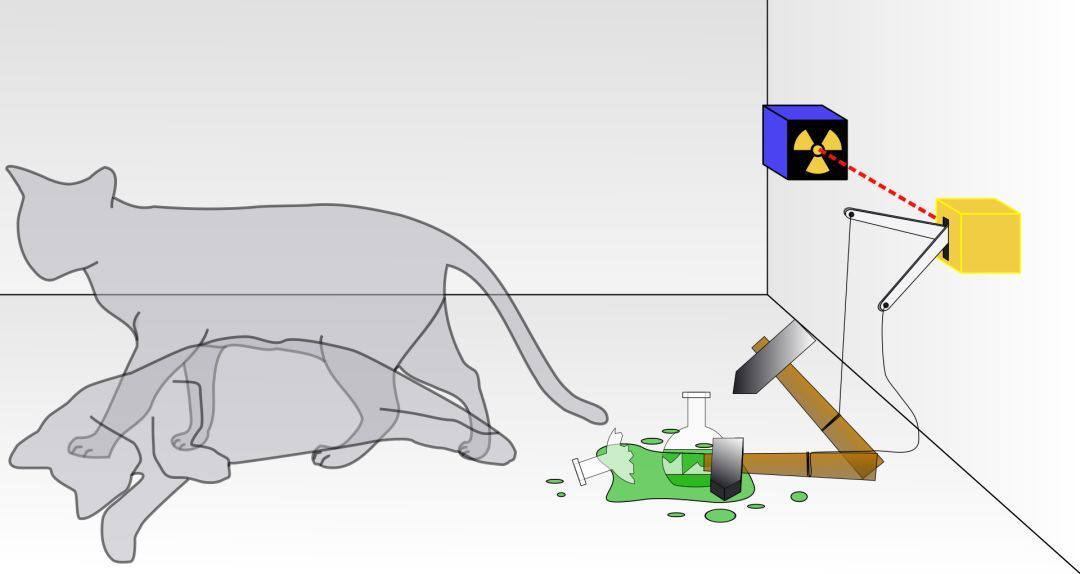
根據(jù)哥本哈根學(xué)派的量子理論,波函數(shù)不能準(zhǔn)確確定電子的位置,,某一時刻的電子,,有可能位于空間中的任何一點,只是位于不同位置的概率不同而已。
換言之,電子在這一時刻的狀態(tài),是由電子在所有固定點的狀態(tài)按一定概率疊加而成的,,稱之為電子的量子“疊加態(tài)”。而每一個固定的點,,被認(rèn)為是電子位置的“本征態(tài)”,。比如在量子理論中,電子的自旋被解釋為電子的內(nèi)在屬性,,無論你從哪個角度來觀察自旋,,都只能得到“上旋”或“下旋”兩種本征態(tài)。那么,,疊加態(tài)就是本征態(tài)按概率的疊加,,兩個概率的組合可以有無窮多。電子既“上”又“下”的疊加態(tài),,是量子力學(xué)中粒子所遵循的根本規(guī)律,。光也是有疊加態(tài)的,例如,,在偏振中,,單個光子的電磁場在垂直和水平方向振蕩,那么光子就是既處于“垂直”狀態(tài)又處于“水平”狀態(tài),。但是,,當(dāng)我們對粒子(比如電子)的狀態(tài)進(jìn)行測量時,電子的疊加態(tài)就不復(fù)存在,,它的自旋要么是“上”,,要么是“下”,。為了解釋這個過程,,海森堡提出了波函數(shù)坍縮的概念,即在人觀察的一瞬間,,電子本來不確定位置的“波函數(shù)”一下子坍縮成某個確定位置的“波函數(shù)”了,。因此,,量子具有不可測量的特性。量子的疊加態(tài),,嚴(yán)重違背了人們的日常經(jīng)驗,,于是薛定諤想出了一個有關(guān)“貓”的思想實驗,以此來嘲笑哥本哈根學(xué)派對“波函數(shù)”概念的概率解釋,。這就是我們耳熟能詳?shù)摹把Χㄖ@的貓”,。他將一只貓關(guān)在裝有少量鐳和氰化物的密閉容器里。鐳的衰變存在幾率,,如果鐳發(fā)生衰變,,會觸發(fā)機(jī)關(guān)打碎裝有氰化物的瓶子,貓就會死,;如果鐳不發(fā)生衰變,,貓就存活。根據(jù)量子力學(xué)理論,,由于放射性的鐳處于衰變和未衰變兩種狀態(tài)的疊加,,因此這只貓相應(yīng)地處于“死”和“活”的疊加狀態(tài),直到有人打開盒子觀測才能有確定的結(jié)果,。薛定諤認(rèn)為,,一只貓,要么是死的,,要么是活的,,怎么可能既死又活?盡管現(xiàn)實中的貓不可能既死又活,,但電子(或原子)的行為就是如此,,這個實驗則使薛定諤再次站到了自己奠基的理論的對立面,因此有物理學(xué)家調(diào)侃道:“薛定諤不懂薛定諤方程,?!?/strong>盡管遭到了薛定諤的反對,但量子疊加態(tài)在上世紀(jì)80年代量子計算誕生后,,已經(jīng)被人們所深信不疑,。1981年5月,物理學(xué)家費曼在麻省理工學(xué)院召開的“物理與計算”會議上做了一個關(guān)于用計算機(jī)模擬量子物理的報告,,他認(rèn)為經(jīng)典計算機(jī)不能準(zhǔn)確模擬量子行為,,需要建造一個按照量子力學(xué)的規(guī)律來運行的計算機(jī)才能成功模擬它。從此,,量子力學(xué)理論被應(yīng)用在計算機(jī)科學(xué)上,,量子計算機(jī)利用的正是量子疊加的特性。經(jīng)典計算使用二進(jìn)制進(jìn)行運算,一個比特總是處于0或1的確定狀態(tài),;量子計算完全不同,,一個量子比特是0和1按照一定概率的疊加。一個量子比特一次就能同時表示0和1兩個數(shù)字,。一個比特只表示一個數(shù)還是同時表示兩個數(shù),,看起來差別不大。但如果多個量子比特與同樣數(shù)目的經(jīng)典比特比較,,差別將是指數(shù)級的,。比如,兩個經(jīng)典比特可以表示00,、01,、10、11這4個數(shù)字,,但只能從中選擇一個,。但如果是兩個量子比特,一次就能同時表示這4個數(shù)字,。再如,,三個經(jīng)典比特仍然只能表示一個數(shù)字,三個量子比特可以用來同時表示8個數(shù)字,。以此類推下去,,隨著比特數(shù)量的增加,經(jīng)典系統(tǒng)一次表示的數(shù)字依然是一個,,只是可以表示的數(shù)值更大而已,。但量子系統(tǒng)同時能表示的數(shù)字?jǐn)?shù)目將以指數(shù)方式快速增加,即2?,。當(dāng)有20個量子比特時,,它一次能表示的數(shù)字?jǐn)?shù)目為22o,超過100萬,。當(dāng)N=250時,,可以表示的數(shù)字?jǐn)?shù)目比宇宙中所有原子的數(shù)目還要多。這就是為什么人們認(rèn)為量子計算機(jī)的計算能力如此強(qiáng)大,。
▍背景簡介:本文摘自公眾號“光子盒”,。